Recent Posts
Archives
«   2025/02   »
일 월 화 수 목 금 토
1
2 3 4 5 6 7 8
9 10 11 12 13 14 15
16 17 18 19 20 21 22
23 24 25 26 27 28
Today
Total
관리 메뉴

Farmer's Golden Life.

[산업기계설비기술사 2차 예상질문 및 답안] CFD에서 Porous Media와 Layer는 무엇인가? 본문

자격증취득/산업기계설비기술사(완)

[산업기계설비기술사 2차 예상질문 및 답안] CFD에서 Porous Media와 Layer는 무엇인가?

Dr. Gold. 2019. 4. 16. 22:34
728x90

[예상질문] CFD에서 Porous Media란 무엇인가?

[답변]

네. 답변드립니다.

먼저 Porous Media은 고체의 Property를 가지지만 내부에 Pore 즉 공간을 가지고 있는 성질의 매체를 의미합니다. 산업에서는 주로 Bag Filter, Flow Distribution(파이프 여러개 연결해 놓은 것), Perforated Metal 등을 해석 할 수 있습니다. 또한 석유가스공학에서는 지하에 존재하는 Natural Gas 또는 석유 시추 분석시 Porous Media 기법을 이용하여 해석할 수 있습니다.


CFD 분석시에는 실제 형상을 3D 모델링을 할 필요없이 Porous Media에 Property를 설정할 수 있습니다. 대표적인 Parameter로는 Permeability가 있으며, Tensile Strength, Electrical Conductivity, Turtuosity 등이 있습니다.

(Tortuosity is a property of a curve being tortuous (twisted; having many turns). There have been several attempts to quantify this property. Tortuosity is commonly used to describe diffusion and fluid flow in porous media, such as soils and snow. -> 한마디로 Porous Media 를 통과하면서 어떻게 Twist되면서 통과하는지에 대한 Property)


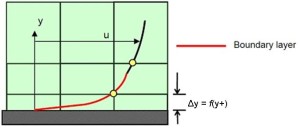
[꼬리질문] CFD에서 Layer는 무엇을 의미하는지요?

CFD에서 Turbulence를 계산할 때. Layer라는 것을 설정하여 계산의 수렴성을 높인다. (Convergency) Layer는 No-Slip Wall 위치에서 부터 벽면으로 부터 거리가 멀어짐에 따라 수치해석이 발산되지 않고, 수렴성을 높이기 위해서 설정하는 중간 계산치라고 볼 수 있다. Layer는 벽면에서 좁은 간격에서 계산이 안정화 되면 넓은 간격으로 계산하도록 설정할 수 있습니다.

여기서 가장 중요한 것은 벽면에서 부터의 처음 Layer인데, 벽면과 가장 가까운 Layer와의 거리를 y+라고 합니다.


Providing a suitable inflation mesh for the geometry is strongly tied to the choice of the turbulence model, and the flow field we are interested in capturing. We can elect to resolve the complete profile of the boundary layer of alternatively we can make use of empirical wall functions to reduce the cell count (see our post on turbulence modelling and wall functions). If we refer to the images below, on the left hand side we observe that the boundary layer profile is modelled with a reduced cell count, which is characteristic of a wall function approach. On the right, the boundary layer profile is resolved all the way to the wall. This will provide a more accurate resolution of the boundary layer. For certain simulations such as flows with strong wall-bounded effects, this resolution is absolutely necessary. For other simulations, the added computational expense is not always justifiable.

wall functions

Representation of Wall Function approach vs fully resolving the boundary layer

At this point, we begin to understand that the placement of the first node in our near-wall mesh is very important.  We use a non-dimensional distance (based on local cell fluid velocity) from the wall to the first node, which we term the y+.  To use a wall function approach for a particular turbulence model with confidence, we need to ensure that our y+ values are within a certain range.  This topic is covered in detail here

y+ definition

This topic will also be discussed more in a future post, but in general it is considered good practice to include between 10 and 15 inflation layers situated within the boundary layer of your flow to accurately resolve the boundary layer and accurately predict any separation or reattachment points.  So now that we understand the importance of inflation layers to our CFD mesh, how can we set them up?

 



A porous medium or a porous material is a material containing pores (voids).[1] The skeletal portion of the material is often called the "matrix" or "frame". The pores are typically filled with a fluid (liquid or gas). The skeletal material is usually a solid, but structures like foams are often also usefully analyzed using concept of porous media.

A porous medium is most often characterised by its porosity. Other properties of the medium (e.g. permeability, tensile strength, electrical conductivity, tortuosity) can sometimes be derived from the respective properties of its constituents (solid matrix and fluid) and the media porosity and pores structure, but such a derivation is usually complex. Even the concept of porosity is only straightforward for a poroelastic medium.

Often both the solid matrix and the pore network (also known as the pore space) are continuous, so as to form two interpenetrating continua such as in a sponge. However, there is also a concept of closed porosity and effective porosity, i.e. the pore space accessible to flow.

Many natural substances such as rocks and soil (e.g. aquifers, petroleum reservoirs), zeolites, biological tissues (e.g. bones, wood, cork), and man made materials such as cements and ceramics can be considered as porous media. Many of their important properties can only be rationalized by considering them to be porous media.

The concept of porous media is used in many areas of applied science and engineering: filtration, mechanics (acoustics, geomechanics, soil mechanics, rock mechanics), engineering (petroleum engineering, bioremediation, construction engineering), geosciences (hydrogeology, petroleum geology, geophysics), biology and biophysics, material science.


7.2.3 Porous Media Conditions

The porous media model can be used for a wide variety of single phase and multiphase problems, including flow through packed beds, filter papers, perforated plates, flow distributors, and tube banks. When you use this model, you define a cell zone in which the porous media model is applied and the pressure loss in the flow is determined via your inputs as described in Section  7.2.3. Heat transfer through the medium can also be represented, subject to the assumption of thermal equilibrium between the medium and the fluid flow, as described in Section  7.2.3.

A 1D simplification of the porous media model, termed the "porous jump,'' can be used to model a thin membrane with known velocity/pressure-drop characteristics. The porous jump model is applied to a face zone, not to a cell zone, and should be used (instead of the full porous media model) whenever possible because it is more robust and yields better convergence. See Section  7.3.20 for details.



Limitations and Assumptions of the Porous Media Model

The porous media model incorporates an empirically determined flow resistance in a region of your model defined as "porous''. In essence, the porous media model is nothing more than an added momentum sink in the governing momentum equations. As such, the following modeling assumptions and limitations should be readily recognized:

  • Since the volume blockage that is physically present is not represented in the model, by default ANSYS FLUENT uses and reports a superficial velocity inside the porous medium, based on the volumetric flow rate, to ensure continuity of the velocity vectors across the porous medium interface. As a more accurate alternative, you can instruct ANSYS FLUENT to use the true (physical) velocity inside the porous medium. See Section  7.2.3 for details. In a multiphase flow system, all phases share the same porosity.

  • The effect of the porous medium on the turbulence field is only approximated. See Section  7.2.3 for details.

  • In general, the ANSYS FLUENT porous medium model, for both single phase and multiphase, assumes the porosity is isotropic, and it can vary with space and time.

  • The Superficial Velocity Formulation and the Physical Velocity Formulation are available for multiphase porous media. See Section  7.2.3 for details.

  • The porous media momentum resistance and heat source terms are calculated separately on each phase. See Section  7.2.3 for details.

  • The interactions between a porous medium and shock waves are not considered.

  • By default, ANSYS FLUENT assumes thermal equilibrium between the porous media solids and multiphase fluid flows. The solids temperature is thus estimated by phase temperatures. However, the solids temperature can also be calculated by a UDS equation (Section  9.1).

  • When applying the porous media model in a moving reference frame, ANSYS FLUENT will either apply the relative reference frame or the absolute reference frame when you enable the Relative Velocity Resistance Formulation. This allows for the correct prediction of the source terms.



Momentum Equations for Porous Media

The porous media models for single phase flows and multiphase flows use the Superficial Velocity Porous Formulation as the default. ANSYS FLUENT calculates the the superficial phase or mixture velocities based on the volumetric flow rate in a porous region. The porous media model is described in the following sections for single phase flow, however, it is important to note the following for multiphase flow:

  • In the Eulerian multiphase model ( this section in the separate Theory Guide), the general porous media modeling approach, physical laws, and equations described below are applied to the corresponding phase for mass continuity, momentum, energy, and all the other scalar equations.

  • The Superficial Velocity Porous Formulation generally gives good representations of the bulk pressure loss through a porous region. However, since the superficial velocity values within a porous region remain the same as those outside the porous region, it cannot predict the velocity increase in porous zones and thus limits the accuracy of the model.

Porous media are modeled by the addition of a momentum source term to the standard fluid flow equations. The source term is composed of two parts: a viscous loss term (Darcy, the first term on the right-hand side of Equation  7.2-1 ) , and an inertial loss term (the second term on the right-hand side of Equation  7.2-1)


S_i = - \left(\sum_{j=1}^3 D_{ij} \mu v_j + \sum_{j=1}^3 C_{ij} \frac{1}{2} \rho \vert v\vert v_j \right) (7.2-1)

where $S_i$ is the source term for the $i$th ( $x$, $y$, or $z$) momentum equation, $\vert v\vert$ is the magnitude of the velocity and $D$ and $C$ are prescribed matrices. This momentum sink contributes to the pressure gradient in the porous cell, creating a pressure drop that is proportional to the fluid velocity (or velocity squared) in the cell.

To recover the case of simple homogeneous porous media


S_i = - \left(\frac{\mu}{\alpha} v_i + C_2 \frac{1}{2} \rho \vert v\vert v_i \right) (7.2-2)

where $\alpha$ is the permeability and $C_2$ is the inertial resistance factor, simply specify $D$ and $C$ as diagonal matrices with $1/\alpha$ and $C_2$, respectively, on the diagonals (and zero for the other elements).

ANSYS FLUENT also allows the source term to be modeled as a power law of the velocity magnitude:


S_i = -C_0 \vert v\vert^{C_1} = -C_0 \vert v\vert^{(C_1-1)}v_i (7.2-3)

where $C_0$ and $C_1$ are user-defined empirical coefficients.

figure   

In the power-law model, the pressure drop is isotropic and the units for $C_0$ are SI.

Darcy's Law in Porous Media

In laminar flows through porous media, the pressure drop is typically proportional to velocity and the constant $C_2$ can be considered to be zero. Ignoring convective acceleration and diffusion, the porous media model then reduces to Darcy's Law:


{\bf\nabla} p = - \frac{\mu}{\alpha} {\vec v} (7.2-4)

The pressure drop that ANSYS FLUENT computes in each of the three ( $x$, $y$, $z$) coordinate directions within the porous region is then


\Delta p_x = \sum_{j=1}^3 \frac{\mu}{\alpha_{xj}} v_j \Delta n_x



\Delta p_y = \sum_{j=1}^3 \frac{\mu}{\alpha_{yj}} v_j \Delta n_y (7.2-5)


\Delta p_z = \sum_{j=1}^3 \frac{\mu}{\alpha_{zj}} v_j \Delta n_z


where $1/{\alpha_{ij}}$ are the entries in the matrix $D$ in Equation  7.2-1, $v_j$ are the velocity components in the $x$, $y$, and $z$ directions, and $\Delta n_x$, $\Delta n_y$, and $\Delta n_z$ are the thicknesses of the medium in the $x$, $y$, and $z$ directions.

Here, the thickness of the medium ( $\Delta n_x$, $\Delta n_y$, or $\Delta n_z$) is the actual thickness of the porous region in your model. Thus if the thicknesses used in your model differ from the actual thicknesses, you must make the adjustments in your inputs for $1/{\alpha_{ij}}$.

Inertial Losses in Porous Media

At high flow velocities, the constant $C_2$ in Equation  7.2-1 provides a correction for inertial losses in the porous medium. This constant can be viewed as a loss coefficient per unit length along the flow direction, thereby allowing the pressure drop to be specified as a function of dynamic head.

If you are modeling a perforated plate or tube bank, you can sometimes eliminate the permeability term and use the inertial loss term alone, yielding the following simplified form of the porous media equation:


{\bf\nabla} p = - \sum_{j=1}^3 C_{2_{ij}} \left (\frac{1}{2} \rho v_j\vert v\vert \right ) (7.2-6)

or when written in terms of the pressure drop in the $x$, $y$, $z$ directions:


$\displaystyle \Delta p_x$$\textstyle \approx$$\displaystyle \sum_{j=1}^3 C_{2_{xj}} \Delta n_x \frac{1}{2} \rho v_{j} \vert v\vert$ 
$\displaystyle \Delta p_y$$\textstyle \approx$$\displaystyle \sum_{j=1}^3 C_{2_{yj}} \Delta n_y \frac{1}{2} \rho v_{j} \vert v\vert$ 
$\displaystyle \Delta p_z$$\textstyle \approx$$\displaystyle \sum_{j=1}^3 C_{2_{zj}} \Delta n_z \frac{1}{2} \rho v_{j} \vert v\vert$(7.2-7)


Again, the thickness of the medium ( $\Delta n_x$, $\Delta n_y$, or $\Delta n_z$) is the thickness you have defined in your model.



Treatment of the Energy Equation in Porous Media

ANSYS FLUENT solves the standard energy transport equation ( this equation in the separate Theory Guide) in porous media regions with modifications to the conduction flux and the transient terms only. In the porous medium, the conduction flux uses an effective conductivity and the transient term includes the thermal inertia of the solid region on the medium:


\frac{\partial}{\partial t} (\gamma \rho_f E_f + (1 - \gam... ... + (\overline{\overline{\tau}} \cdot {\vec v}) \right] + S^h_f (7.2-8)

where


$E_f$=total fluid energy
$E_s$=total solid medium energy
$\gamma$=porosity of the medium
$k_{\rm eff}$=effective thermal conductivity of the medium
$S^h_f$=fluid enthalpy source term


Effective Conductivity in the Porous Medium

The effective thermal conductivity in the porous medium, $k_{\rm eff}$, is computed by ANSYS FLUENT as the volume average of the fluid conductivity and the solid conductivity:


k_{\rm eff} = \gamma k_f + (1-\gamma)k_s (7.2-9)

where


$\gamma$=porosity of the medium
$k_f$=fluid phase thermal conductivity (including the turbulent contribution, $k_t$)
$k_s$=solid medium thermal conductivity


The fluid thermal conductivity $k_f$ and the solid thermal conductivity $k_s$ can be computed via user-defined functions.

The anisotropic effective thermal conductivity can also be specified via user-defined functions. In this case, the isotropic contributions from the fluid, $\gamma k_f$, are added to the diagonal elements of the solid anisotropic thermal conductivity matrix.

저작자표시 비영리 변경금지

'자격증취득 > 산업기계설비기술사(완)' 카테고리의 다른 글

[산업기계설비기술사 2차 예상질문 및 답안] 볼트의 호칭치수를 설명해보세요.  (0) 2019.04.17
[산업기계설비기술사 2차 예상질문 및 답안] 유압시스템은 보통 어떻게 이루어 지나요?  (0) 2019.04.16
[산업기계설비기술사 2차 예상질문 및 답안] Newtonian Fluid가 무엇인가요?  (0) 2019.04.15
[산업기계설비기술사 2차 예상질문 및 답안] CFD와 수계산시 압력 저하는 어느게 더 높냐?  (0) 2019.04.15
[산업기계설비기술사 2차 예상질문 및 답안] Standard/Code/Specification의 차이점  (0) 2019.04.15
'자격증취득/산업기계설비기술사(완)' Related Articles more

Comments